いろいろ 三角形の角度の�� なぜ 974600-三角形の角度��和 なぜ
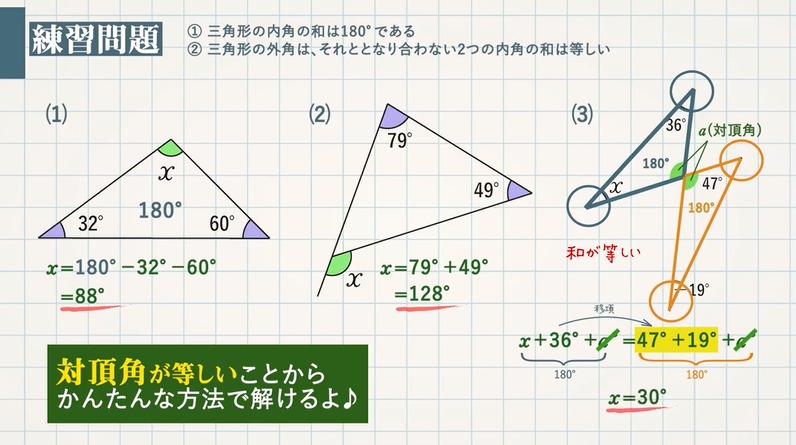
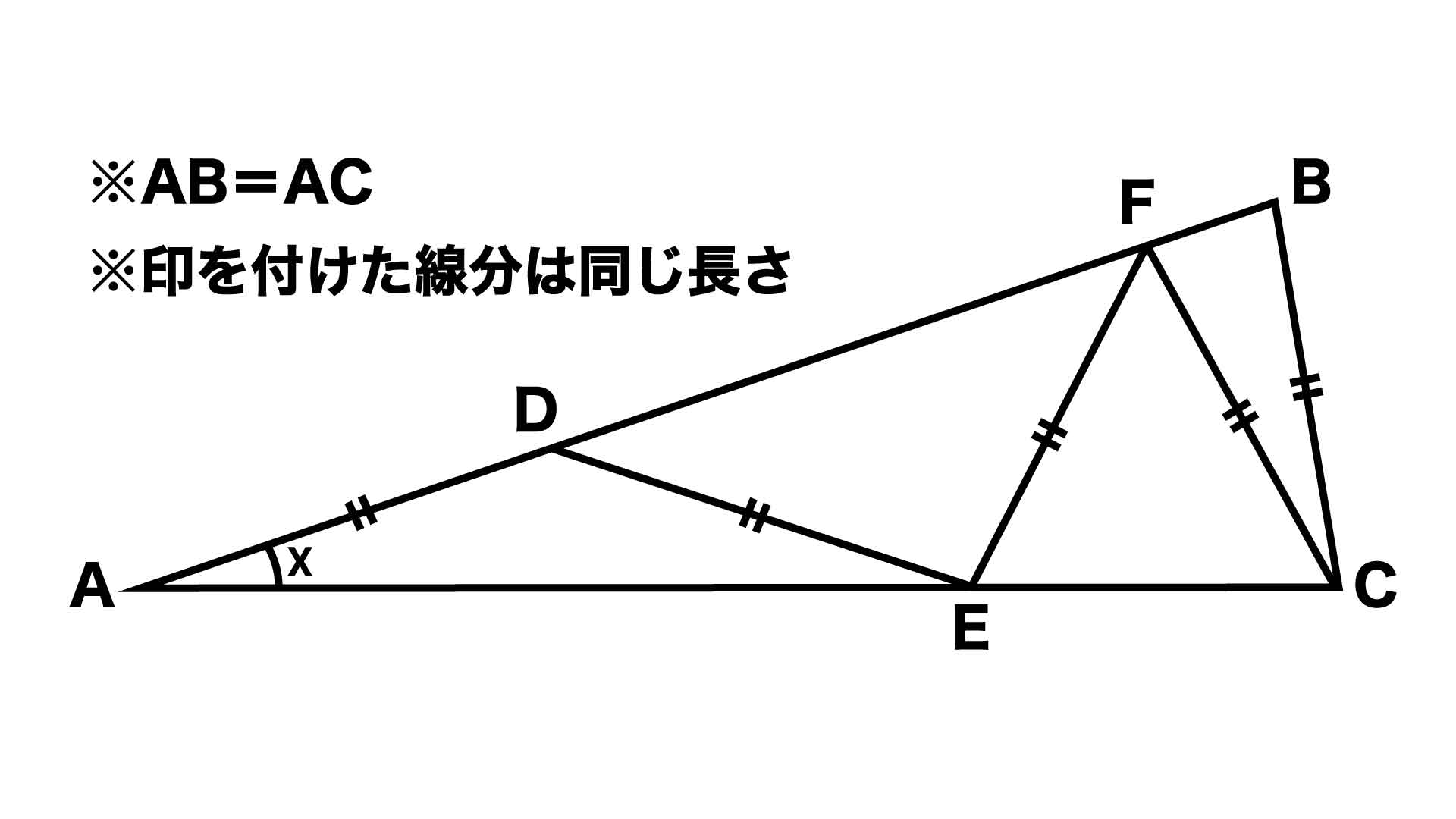
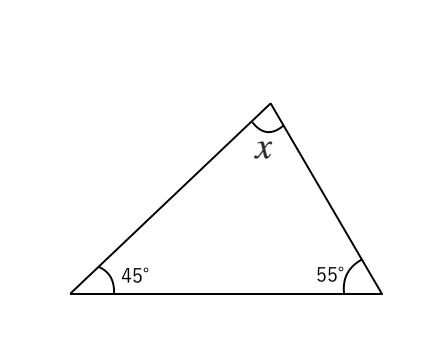
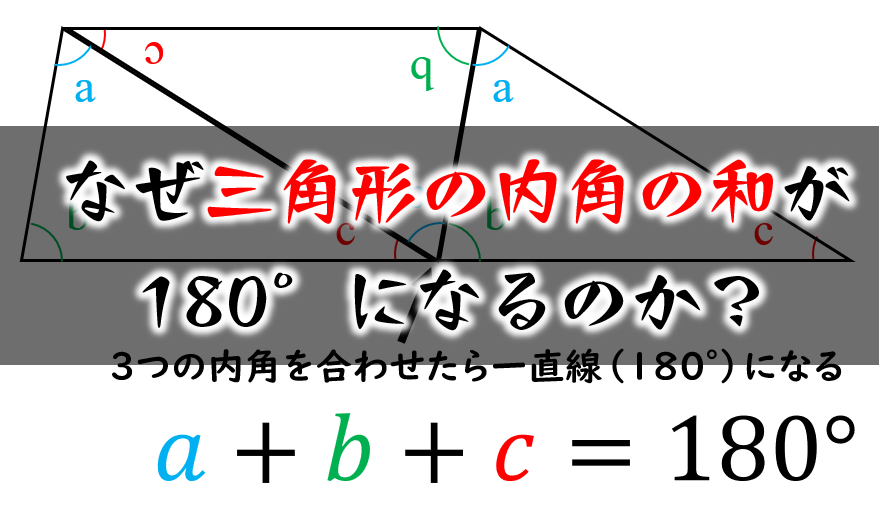
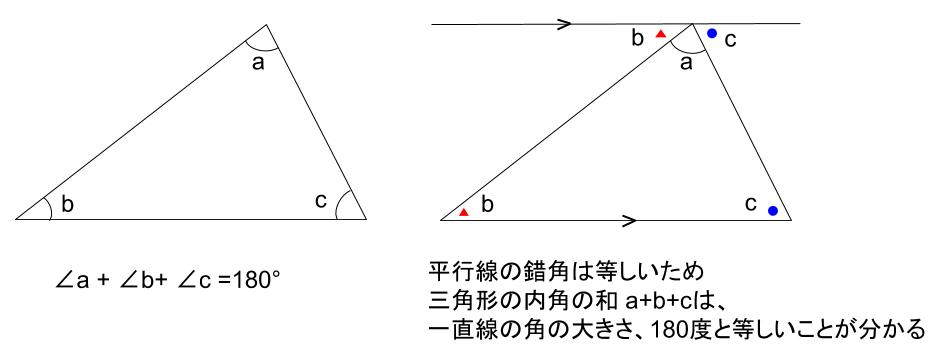
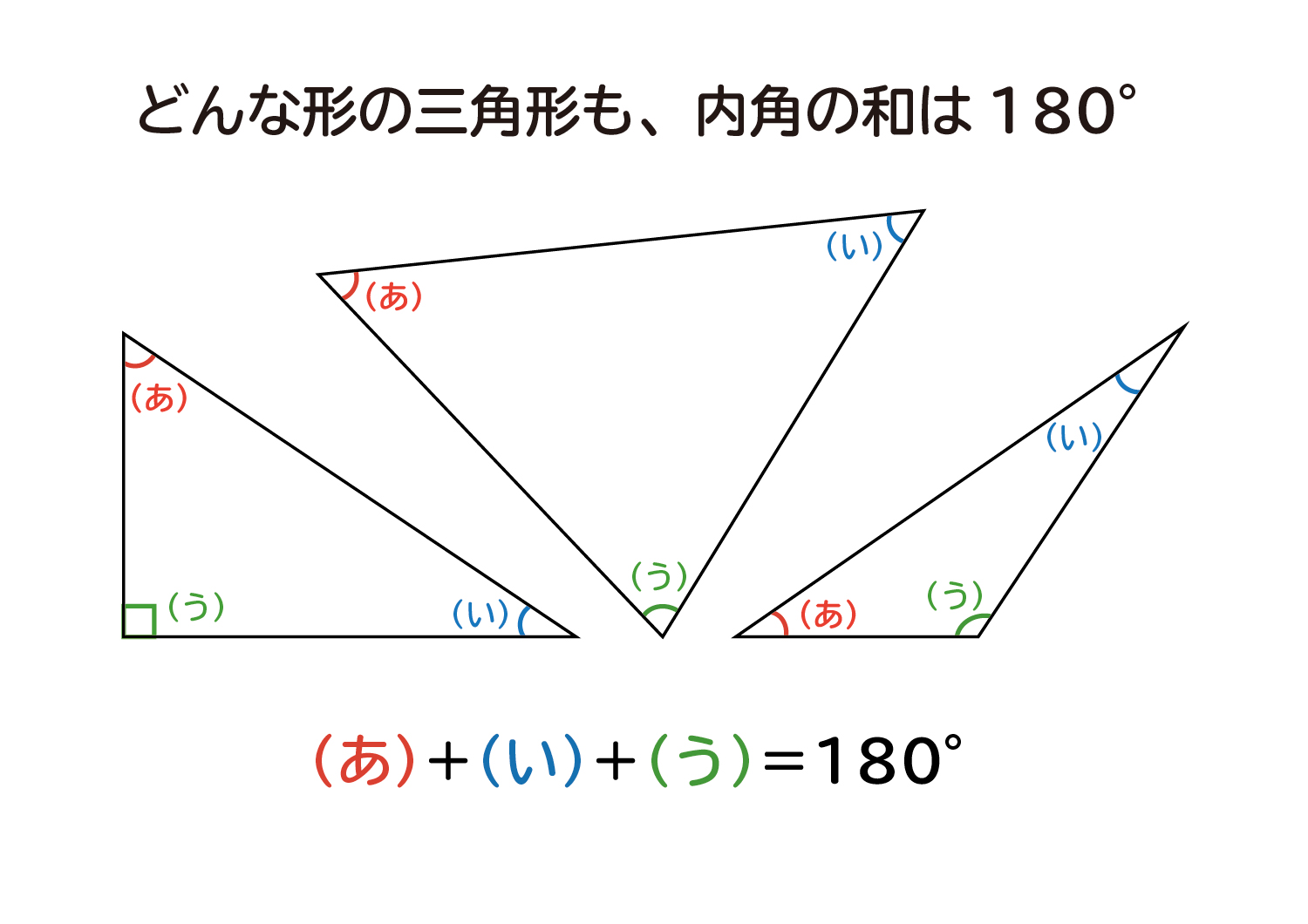
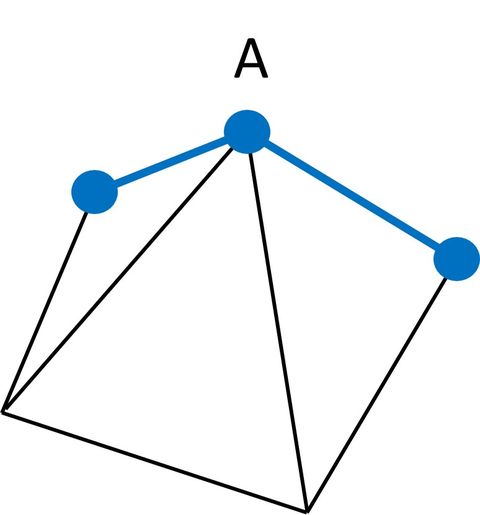
なんと、ACを軸にして、折り返すように三角形をもう一つ書くと、黄色い三角形が現れたね! もうわかったかな? あとは、黄色い三角形の内角の和が180°であることを利用して $ x = 180 – ( 60 ) – 50 = 30$ 答えは出たね! でも、これで終わりではない
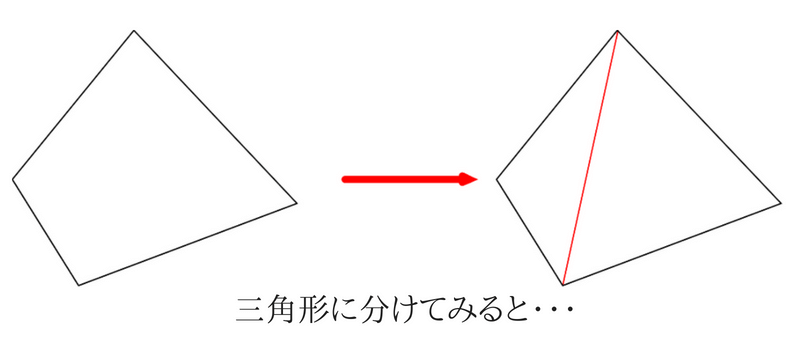
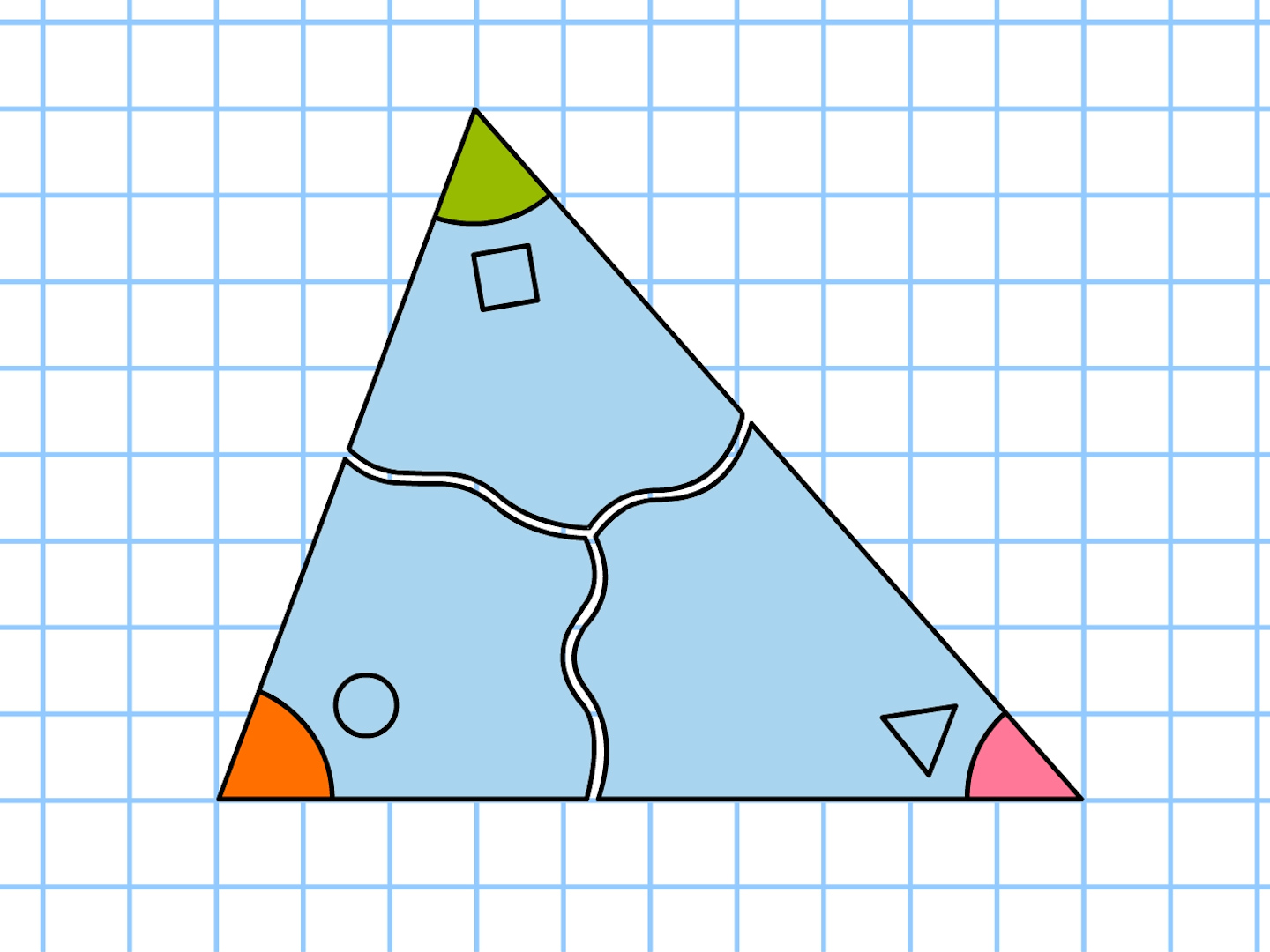
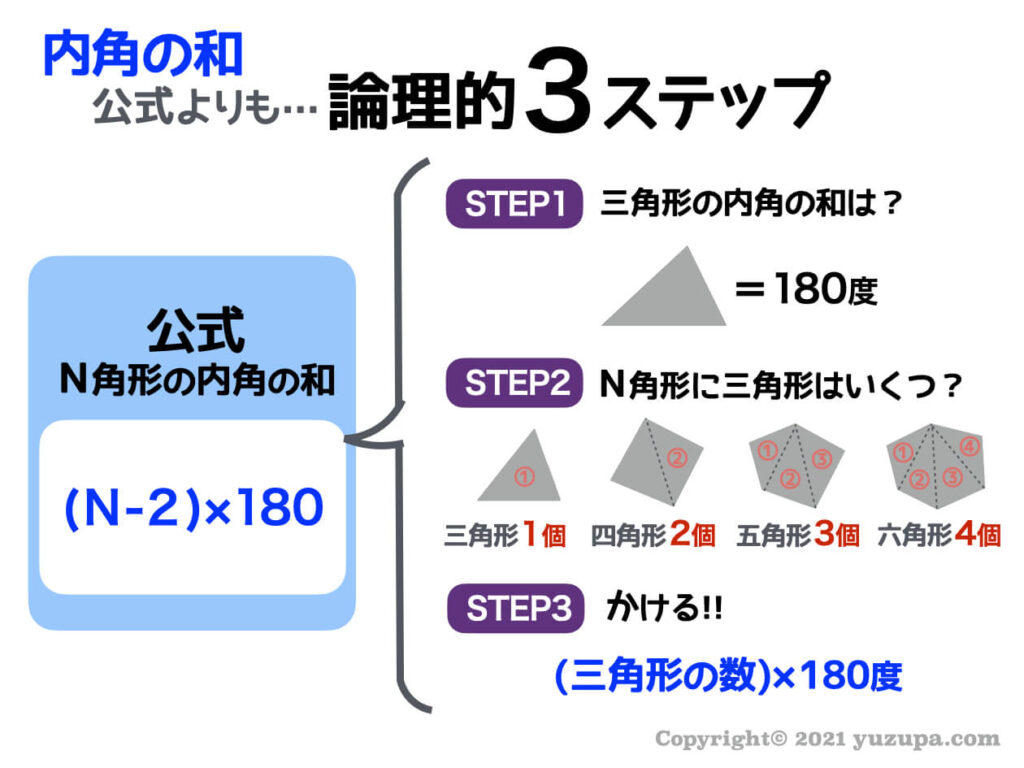
三角形の角度の和 なぜ-1 三角形の内角の和は180°になる 11 なぜ3つの角度をたすと180°になるのか 12 三角形の種類:正三角形、二等辺三角形、直角三角形 2 四角形の内角の和は360°になる 21 対角線を引くと、内角の和が360°になる理由がわかる 22 重要な四角形が正方形と三角形の種類 三角形は内角の大きさによって三種類に分けられます。 鋭角三角形 (えいかくさんかっけい) すべての角が90度より小さい三角形です。 直角三角形 (ちょっかくさんかっけい) 90度ちょうどの角がある三角形を直角三角形といいます。
三角形の角度の和 なぜのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
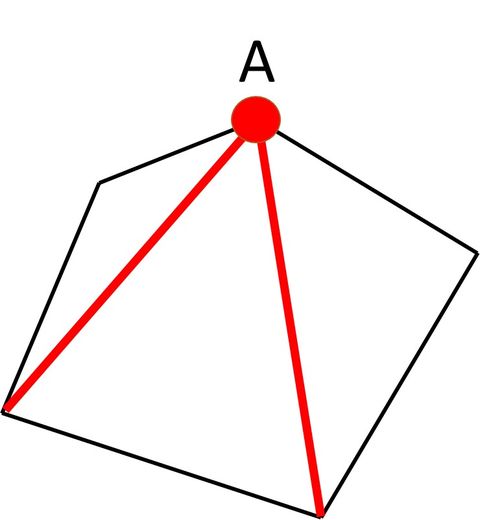
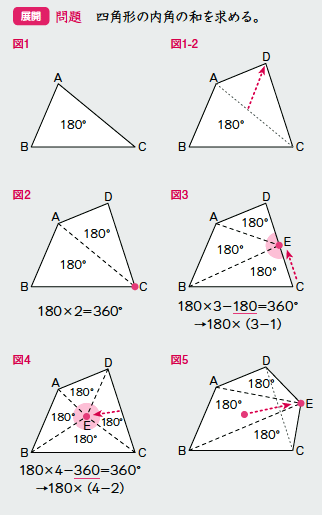
 |  | |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「三角形の角度の和 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | 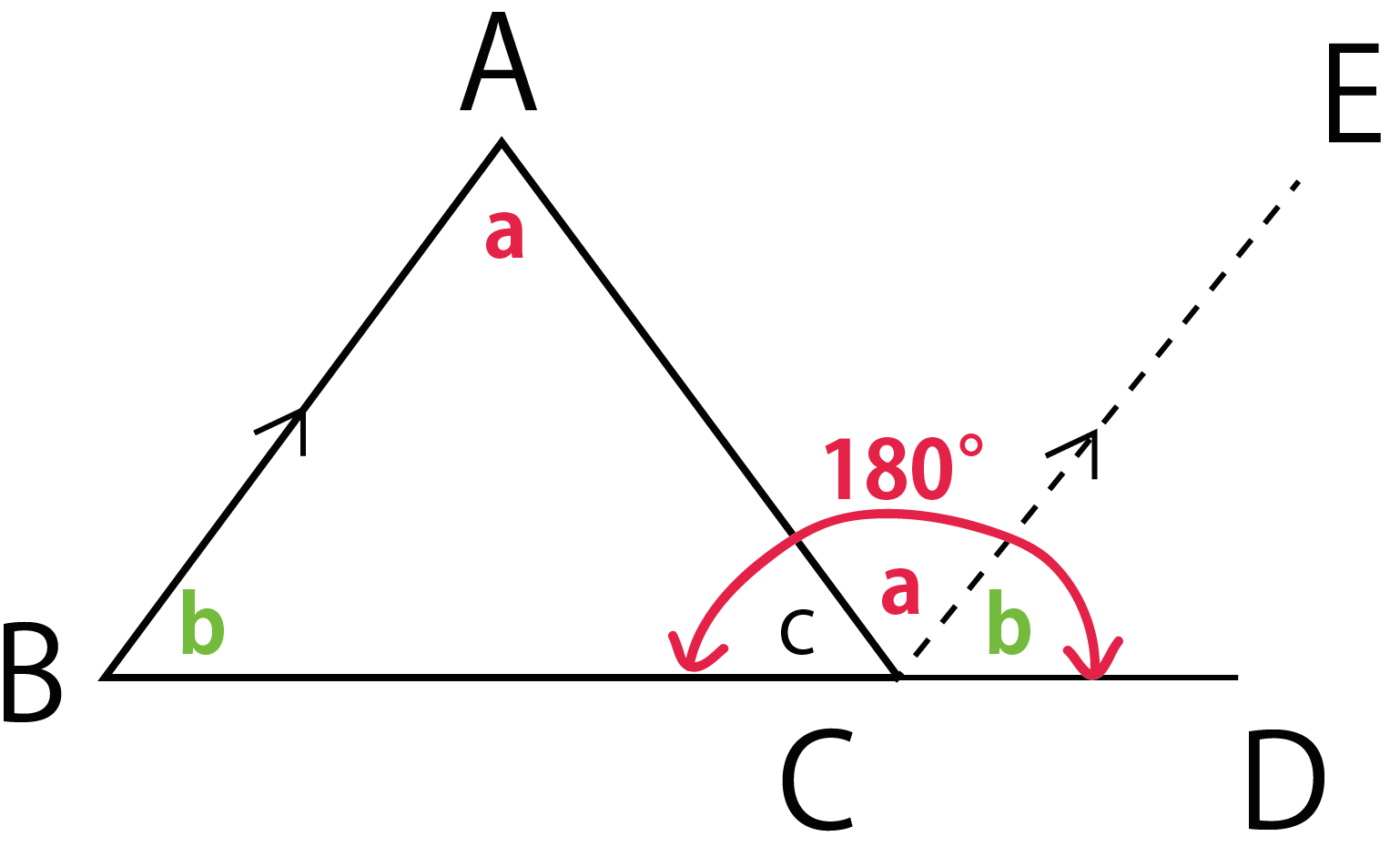 |
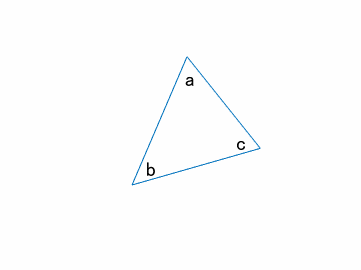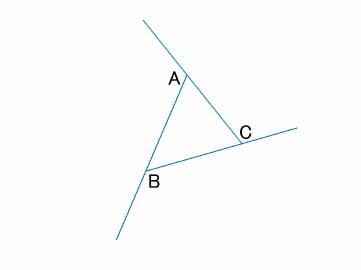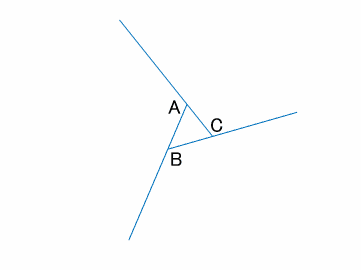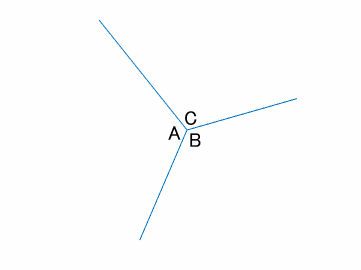
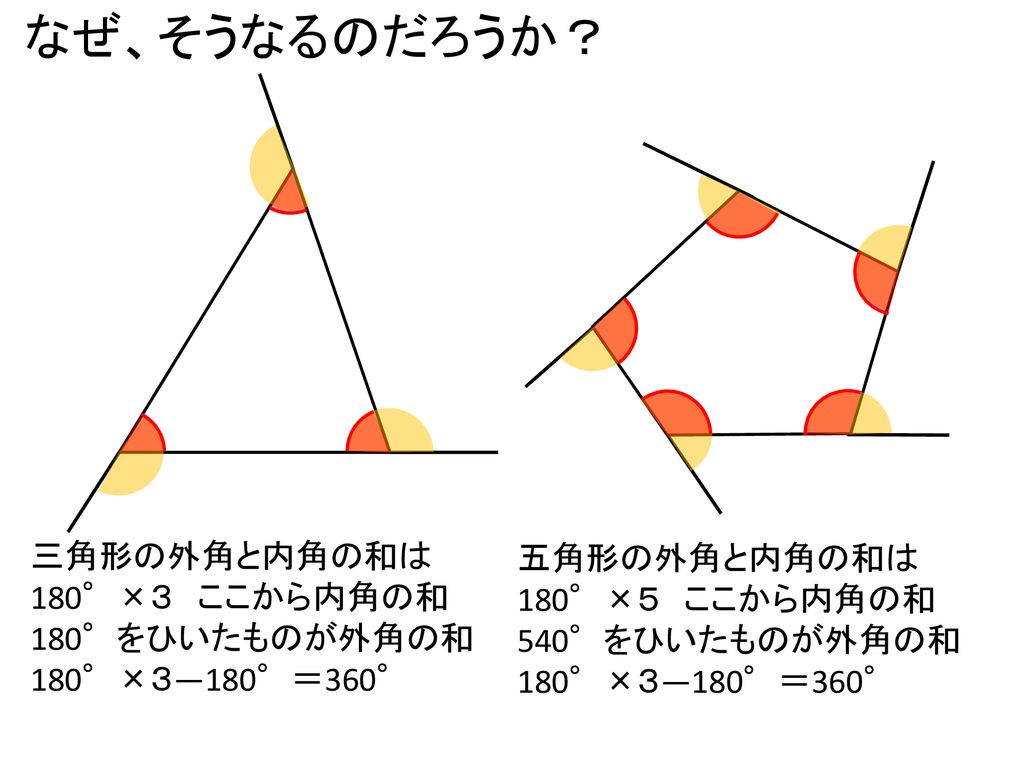
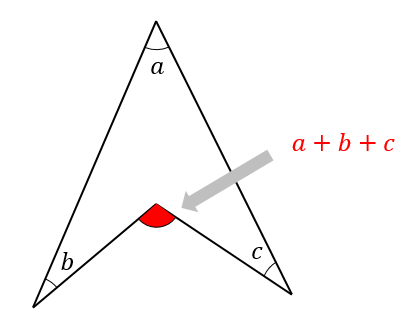
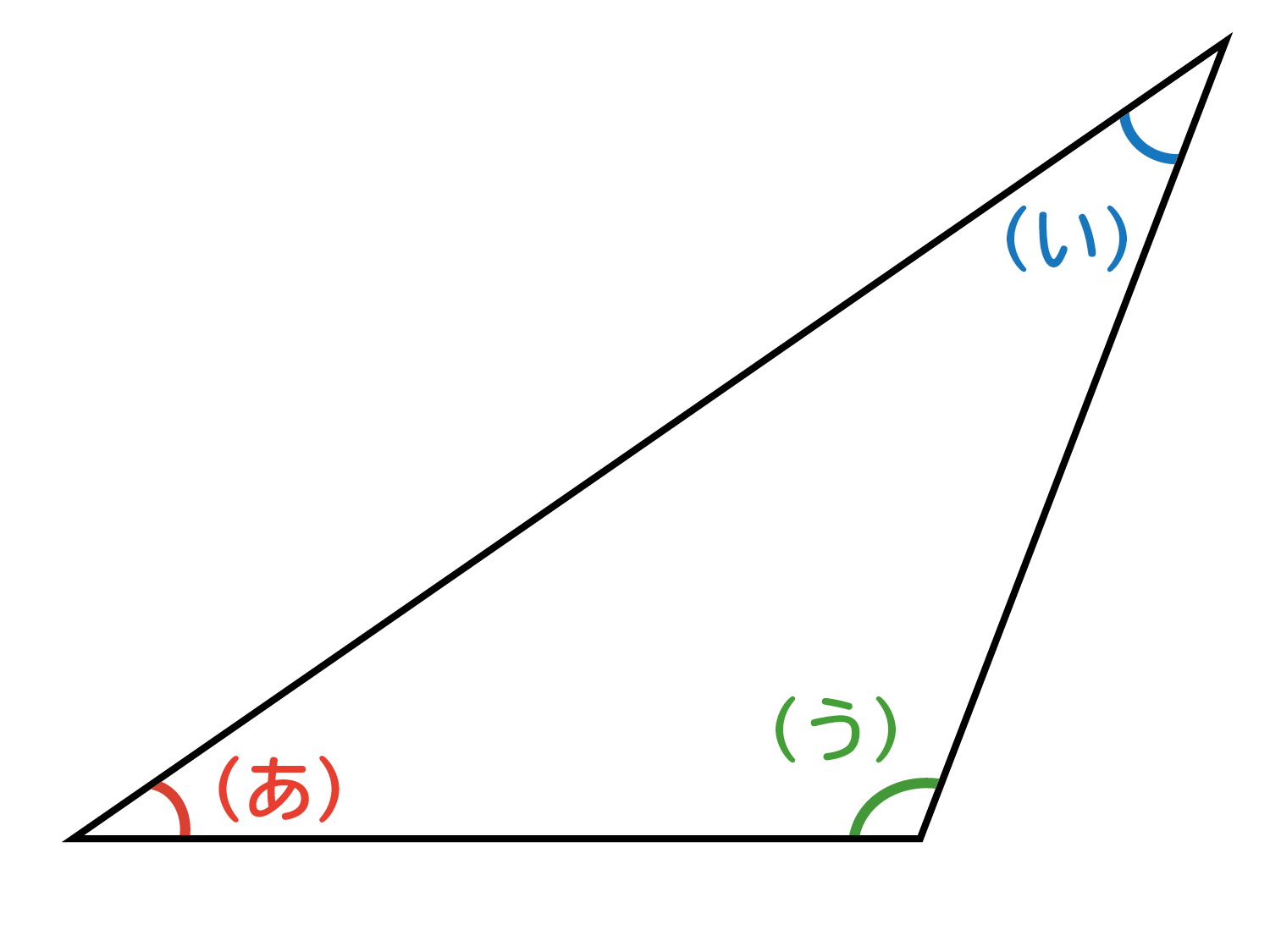
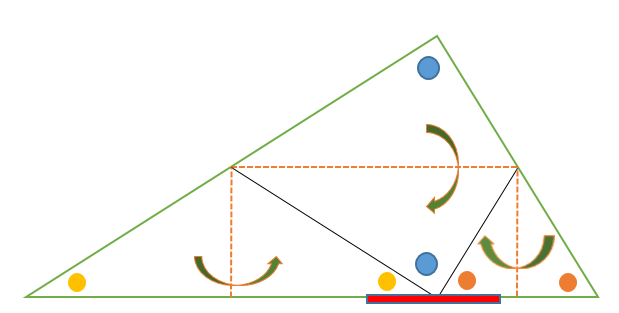
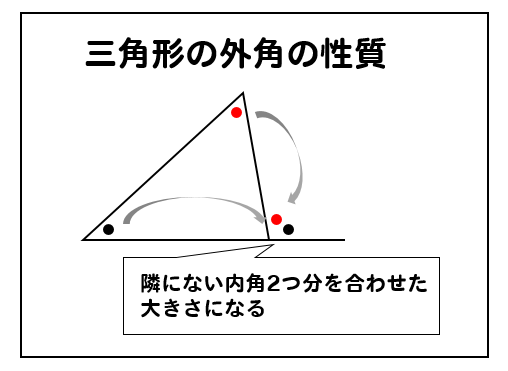
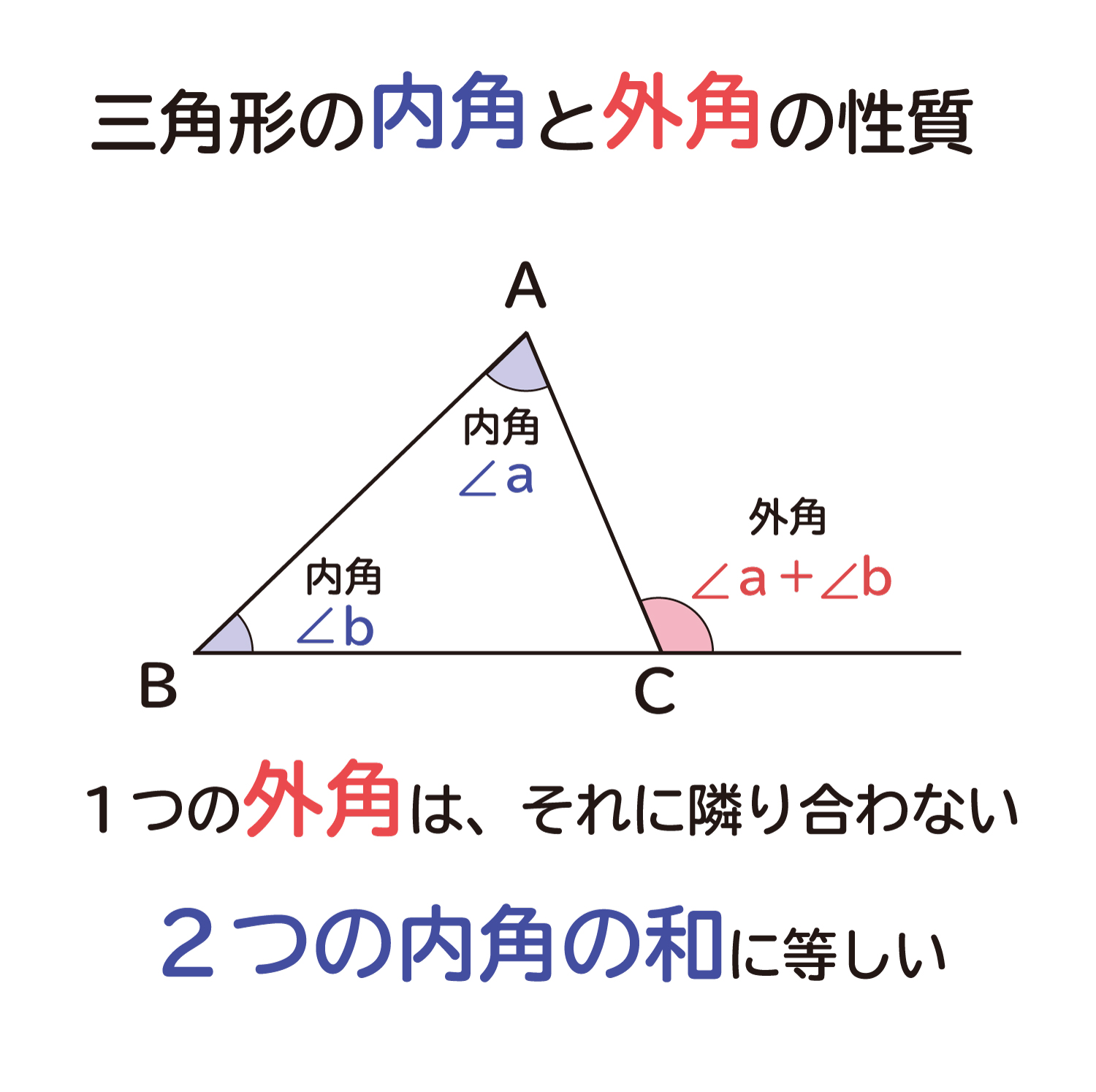
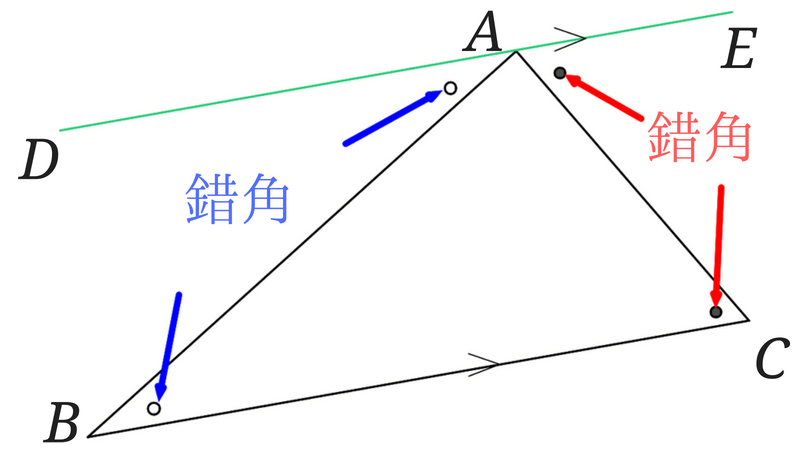
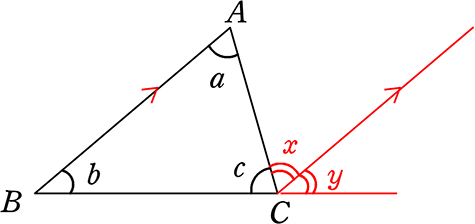
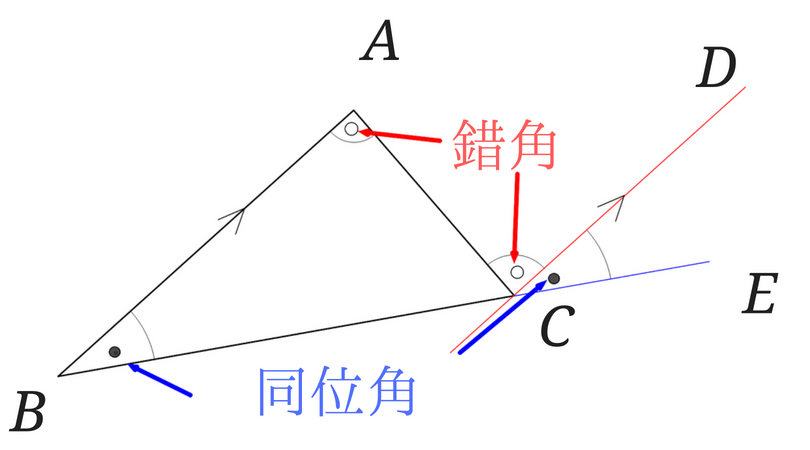
図 1 でいえば、∠abc が内角の 1 つとなる。三角形は 3 つの内角をもち、その和は平面上では2直角( 180 度)となる(本稿はユークリッド幾何学における三角形を論じる)。 また、∠acd のように 1 つの辺と他の辺の延長との間にできる角を三角形の外角という。 球面上の三角形の内角の和 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明できました。ここで,任意の三角形に対して面積 s > 0 s > 0 s > 0 なので a b c > π abc > \pi a b c > π が成立します! つまり, 球面上の三角形の内角の和は π \pi π より
Incoming Term: 三角形の角度の和 なぜ,
コメント
コメントを投稿